-
论坛网址:https://db2.mom(可微信分享)、https://0668.es、https://0668.cc(全加密访问)
您正在使用一款已经过时的浏览器!部分功能不能正常使用。
请尝试升级或使用 其他浏览器。
请尝试升级或使用 其他浏览器。
数学老师呢~ (6人在浏览)
- 主题发起人 天空蔚蓝
- 开始时间
QUOTE(铺路石 @ 2014年12月06日 Saturday, 10:02 PM)
3部分和4部分你怎么会想到相等呢?你都想当然地把那个未知数当60了
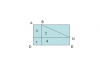
五边形ABNED面积=五边形NEDAB面积
1部分面积和2部分面积是相同的,所以3部分面积=4部分面积
这样答案更简单了,3部分面积=40*30=1200平方米
所以阴影面积=1200*2+20*30=3000平方米
请不要再随便看网上说什么条件不足不能解,也不要说无解了,还有什么长度变长之类的。怎么变都可以解出来,
当然,本题是不能变的,变就不是原来题目
3部分和4部分你怎么会想到相等呢?你都想当然地把那个未知数当60了
[snapback]3720623[/snapback]
五边形ABNED面积=五边形NEDAB面积
1部分面积和2部分面积是相同的,所以3部分面积=4部分面积
这样答案更简单了,3部分面积=40*30=1200平方米
所以阴影面积=1200*2+20*30=3000平方米
请不要再随便看网上说什么条件不足不能解,也不要说无解了,还有什么长度变长之类的。怎么变都可以解出来,
当然,本题是不能变的,变就不是原来题目
相似主题
正在浏览此帖子的用户
当前在线: 7 (会员: 0, 游客: 7)